

These relations may be used to solve inequalities involving absolute values. Two other useful properties concerning inequalities are: $$|a| ≤ b ⇔ -b ≤ a ≤ b$$ $$|a| ≥ b ⇔ a ≤ -b \space or \space b ≤ a$$ Idempotence (the absolute value of the absolute value is the absolute value) $$||a|| = |a|$$ Symmetry $$|-a| = |a|$$ Identity of indiscernibles (equivalent to positive-definiteness) $$|a - b| = 0 ⇔ a = b$$ Triangle inequality (equivalent to subadditivity) $$|a - b| ≤ |a - c| + |c - b|$$ Preservation of division (equivalent to multiplicativeness) $$|a / b| = |a| / |b| \space\space if \space\space b ≠ 0$$ (equivalent to subadditivity) $$|a - b| ≥ ||a| - |b||$$ Other important properties of the absolute value include: Álgebra (todo el contenido) Unidad: Ecuaciones de valor absoluto, funciones y desigualdades Ups. The absolute value has the following four fundamental properties: I'll solve to find that interval: x 3 > 0 x > 3 The argument of this absolute value will be negative before the breakpoint (at x 3) and positive after.

Furthermore, the absolute value of the difference of two real numbers is the distance between them. The first absolute-value expression, in the left-hand side of the equation, is positive when the argument is positive. The absolute value of a number may be thought of as its distance from zero along real number line. The absolute value (or modulus) | x | of a real number x is the non-negative value of x without regard to its sign.įor example, the absolute value of 5 is 5, and the absolute value of −5 is also 5.
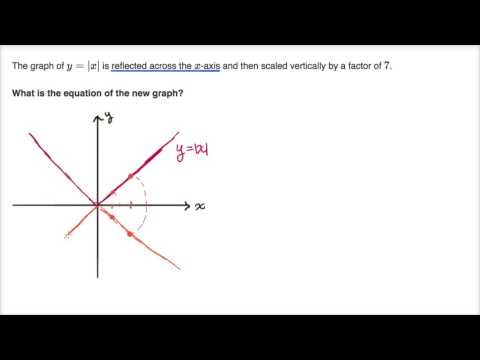
Solve the Quadratic Equation by the Quadratic Formula.Solve the Quadratic Equation by Factoring.Solve the Quadratic Equation by Extracting Roots.Multiplying and Dividing Positive and Negative Whole Numbers.\) and that the graph has been reflected vertically. To solve absolute value equations, find x values that make the expression inside the absolute value positive or negative the constant.


 0 kommentar(er)
0 kommentar(er)
